Programmable Matter
In the field of programmable matter we consider materials that can change their physical properties such as shape, elasticity, conductivity, or color, based on programmable behavior and reacting to external influences. Various interpretations of programmable matter have been portrayed in popular science fiction, and there are many possible applications for such materials: Minimally invasive medical treatment, monitoring and repairing buildings and machines, advanced manufacturing, or exploration of hazardous or obstructed environments.
We view programmable matter as large systems of tiny particles with limited locomotion, computation and communication abilities. With recent advances in micro- and nanorobotics, it seems likely that the production of such particles will be possible within the next few decades.
In our research, we study programmable matter from a theoretical perspective. In order to program the particles in such a way that arbitrarily large numbers of them can cooperate to achieve complex goals in a reasonable time, the fundamental capabilities and limitations of such systems must be explored. Therefore, we use abstract mathematical models to focus on the most important aspects of programmable matter systems. Such models allow us to precisely formulate assumptions on the particles' abilities and rigorously analyze the correctness and runtime of algorithms. By these means, we explore under which assumptions the fundamental coordination problems can be solved and develop efficient distributed algorithms, building a theoretical foundation for future physical implementations.
The Amoebot Model
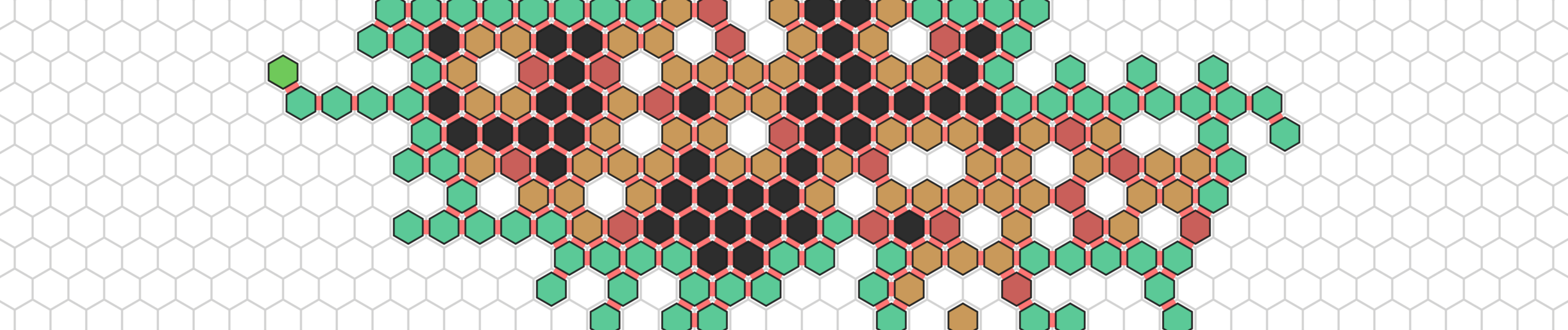
Our work is mainly based on the so-called amoebot model of programmable matter, which we introduced and continue to develop in collaboration with other researchers (see list of publications below). This model was inspired by amoeba, single-celled organisms that move by expanding and contracting their bodies.
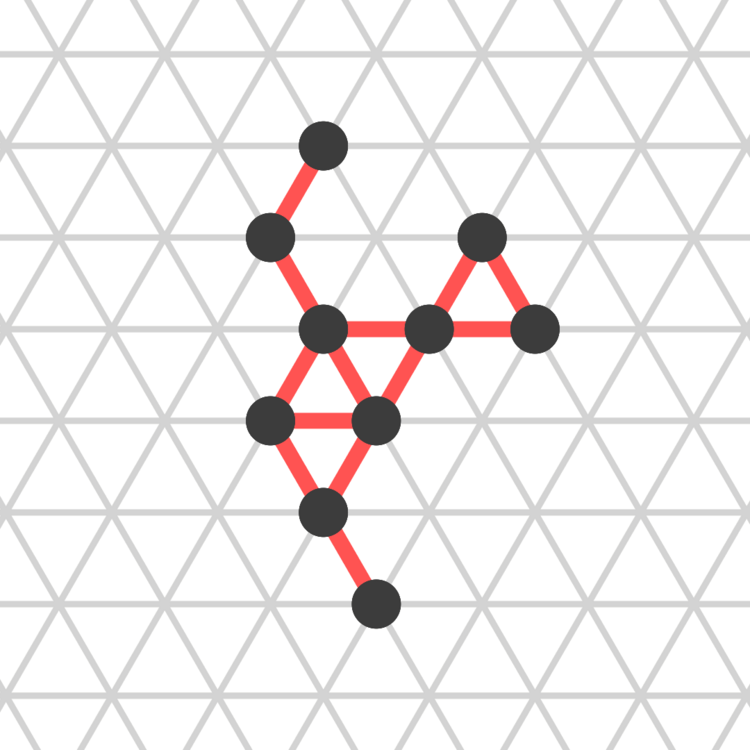
In the amoebot model, we call the particles amoebots and place them on the nodes of a graph such that every node is occupied by at most one amoebot. For example, in the popular geometric variant of the model, we place a set of n amoebots on the infinite regular triangular grid graph. Each amoebot initially occupies one node. By performing an expansion, an amoebot occupying a node v can expand onto an adjacent unoccupied node w, after which it occupies both nodes v and w. The expanded amoebot can then perform a contraction to contract onto either v or w, after which it only occupies one node again. Through repeated expansions and contractions, the amoebots can move through the graph.
When two amoebots occupy adjacent nodes, they can exchange information to communicate. The amoebots are controlled by finite state machines and we typically assume that the number of states does not grow with the number of amoebots. This means that amoebots cannot compute unique identifiers and the exchange of information is very limited.
In this model, we studied the leader election problem, where the amoebots have to agree on a unique leader amoebot, shape formation algorithms, allowing the amoebots to reorganize themselves into predefined shapes from any initial configuration, and other common problems for self-coordinating robotic systems.
Model Extensions
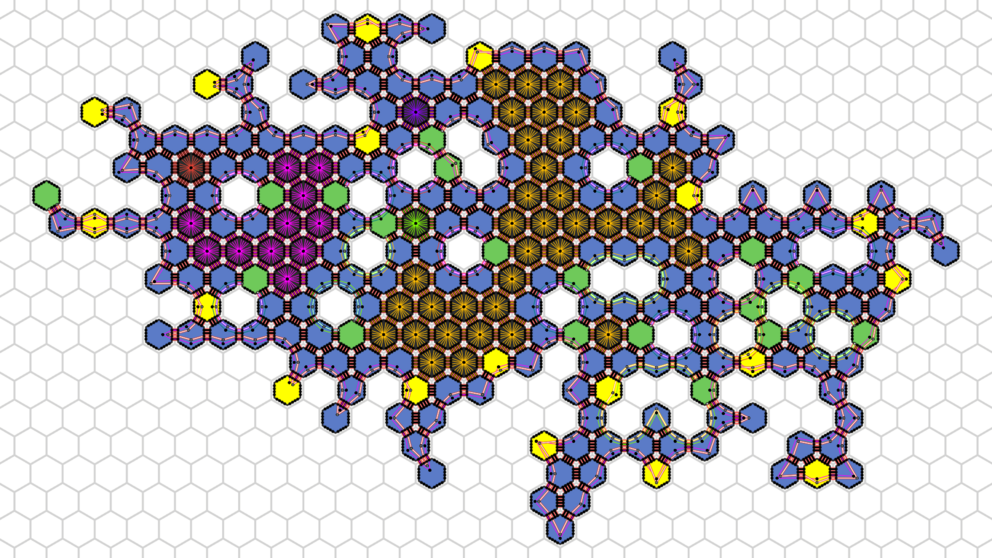
Due to the local communication and movement constraints, many algorithms in the amoebot model require a runtime that grows at least linearly with the number of amoebots, which is generally too slow for real applications with many particles. This problem motivated two extensions of the amoebot model: Reconfigurable circuits and joint movements.
The reconfigurable circuit extension allows amoebots to construct communication networks, so-called circuits, on connected subgraphs of the amoebot structure. On the circuits, they can send primitive signals called beeps, which are transmitted instantaneously to all amoebots connected by a circuit. This extension allows much more efficient solutions for leader election and other problems, such as constructing spanning trees and shortest path forests.
The joint movement extension enables amoebots to push and pull each other with their contractions and expansions. Thereby, a chain of amoebots that expands together can cover a much greater distance than if all amoebots move separately from each other. This extension allows for rapid shape transformations and fast locomotion of an amoebot structure along a surface, but it introduces new coordination challenges to avoid collisions and conflicting movements.
The two extensions were inspired by the nervous and muscular system and are designed to work together. We hope to utilize communication via circuits to solve the coordination problems of joint movements and ultimately develop much more efficient shape formation algorithms.
Amoebot Simulator
Amoebot Model Publications
The canonical amoebot model: algorithms and concurrency control
J.J. Daymude, A.W. Richa, C. Scheideler, Distributed Comput. 36 (2023) 159–192.
Fault-Tolerant Shape Formation in the Amoebot Model
I. Kostitsyna, C. Scheideler, D. Warner, in: T.E. Ouldridge, S.F.J. Wickham (Eds.), 28th International Conference on DNA Computing and Molecular Programming (DNA 28), Schloss Dagstuhl – Leibniz-Zentrum für Informatik, Dagstuhl, Germany, 2022, p. 9:1–9:22.
Convex Hull Formation for Programmable Matter
J.J. Daymude, R. Gmyr, K. Hinnenthal, I. Kostitsyna, C. Scheideler, A.W. Richa, in: Proceedings of the 21st International Conference on Distributed Computing and Networking, 2020.
On the runtime of universal coating for programmable matter
J. J. Daymude, Z. Derakhshandeh, R. Gmyr, A. Porter, A. W. Richa, C. Scheideler, T.F. Strothmann, Natural Computing (2018) 81--96.
Improved Leader Election for Self-organizing Programmable Matter
J. J. Daymude, R. Gmyr, A. W. Richa, C. Scheideler, T.F. Strothmann, in: Algorithms for Sensor Systems - 13th International Symposium on Algorithms and Experiments for Wireless Sensor Networks, ALGOSENSORS 2017, Vienna, Austria, September 7-8, 2017, Revised Selected Papers, 2017, pp. 127--140.
Universal Shape Formation for Programmable Matter
Z. Derakhshandeh, R. Gmyr, A. W. Richa, C. Scheideler, T.F. Strothmann, in: Proceedings of the 28th ACM Symposium on Parallelism in Algorithms and Architectures, SPAA 2016, Asilomar State Beach/Pacific Grove, CA, USA, July 11-13, 2016, ACM, 2016, pp. 289--299.
Leader Election and Shape Formation with Self-organizing Programmable Matter
Z. Derakhshandeh, R. Gmyr, T.F. Strothmann, R. A. Bazzi, A. W. Richa, C. Scheideler, in: DNA Computing and Molecular Programming - 21st International Conference, DNA 21, Boston and Cambridge, MA, USA, August 17-21, 2015. Proceedings, 2015, pp. 117--132.
Brief announcement: amoebot - a new model for programmable matter
Z. Derakhshandeh, S. Dolev, R. Gmyr, A. W. Richa, C. Scheideler, T.F. Strothmann, in: 26th ACM Symposium on Parallelism in Algorithms and Architectures, SPAA’14, Prague, Czech Republic - June 23 - 25, 2014, ACM, 2014, pp. 220--222.
Show all publications
Model Extensions
The structural power of reconfigurable circuits in the amoebot model
A. Padalkin, C. Scheideler, D. Warner, Natural Computing (2024).
Reconfiguration and Locomotion with Joint Movements in the Amoebot Model
A. Padalkin, M. Kumar, C. Scheideler, in: A. Casteigts, F. Kuhn (Eds.), 3rd Symposium on Algorithmic Foundations of Dynamic Networks, SAND 2024, June 5-7, 2024, Patras, Greece, Schloss Dagstuhl - Leibniz-Zentrum für Informatik, 2024, p. 18:1–18:20.
Polylogarithmic Time Algorithms for Shortest Path Forests in Programmable Matter
A. Padalkin, C. Scheideler, in: Proceedings of the 43rd ACM Symposium on Principles of Distributed Computing, ACM, 2024.
Coordinating Amoebots via Reconfigurable Circuits
M. Feldmann, A. Padalkin, C. Scheideler, S. Dolev, J. Comput. Biol. 29 (2022) 317–343.
Show all publications
Related Papers
Efficient Shape Formation by 3D Hybrid Programmable Matter: An Algorithm for Low Diameter Intermediate Structures
K. Hinnenthal, D.J. Liedtke, C. Scheideler, in: A. Casteigts, F. Kuhn (Eds.), 3rd Symposium on Algorithmic Foundations of Dynamic Networks (SAND 2024), Schloss Dagstuhl – Leibniz-Zentrum für Informatik, Dagstuhl, Germany, 2024, p. 15:1–15:20.
Universal Coating by 3D Hybrid Programmable Matter
I. Kostitsyna, D.J. Liedtke, C. Scheideler, in: Y. Emek (Ed.), Structural Information and Communication Complexity, Springer Nature Switzerland, Cham, 2024.
Algorithmic Foundations of Programmable Matter Dagstuhl Seminar 16271
S. P. Fekete, A. W. Richa, K. Römer, C. Scheideler, SIGACT News (2017) 87--94.
Show all publications