Algorithmic geometry

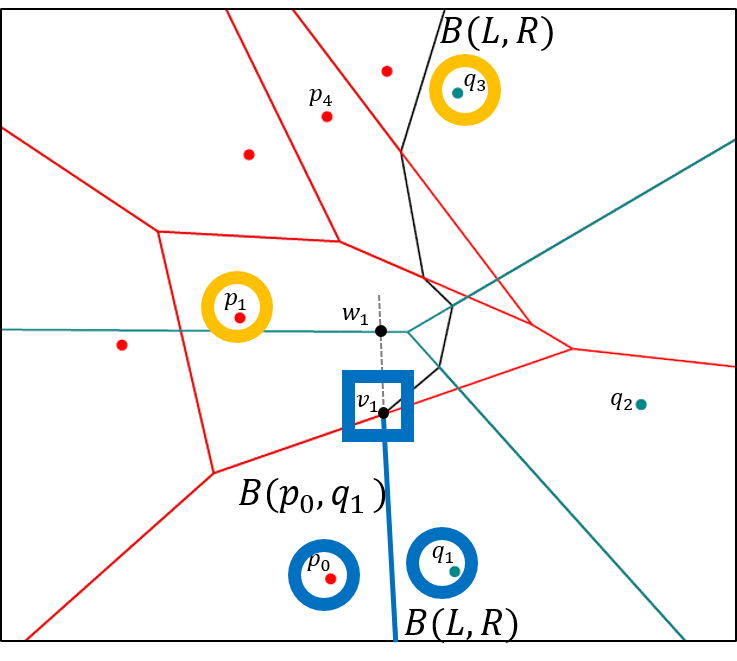
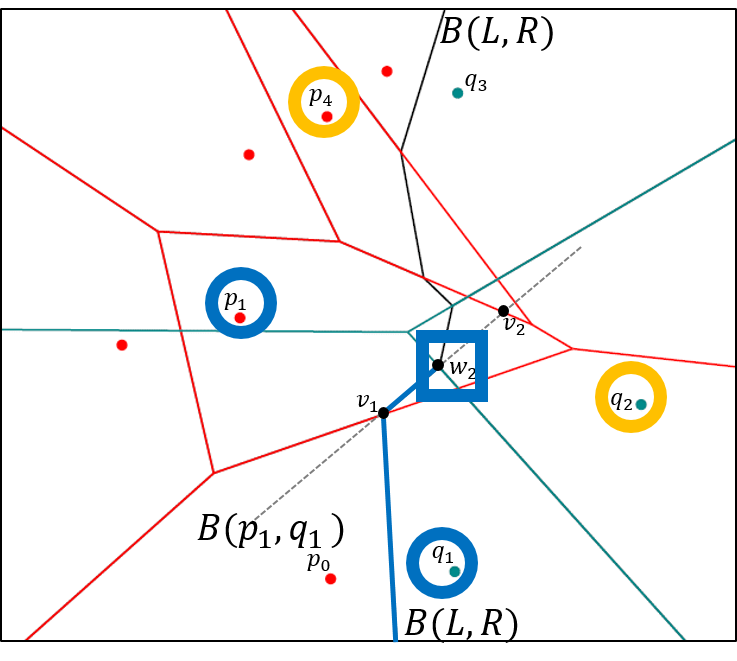
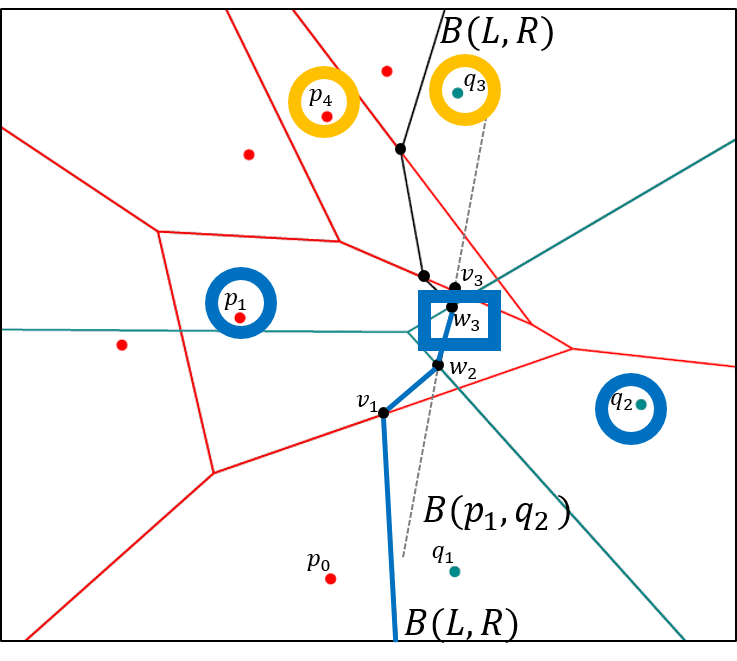
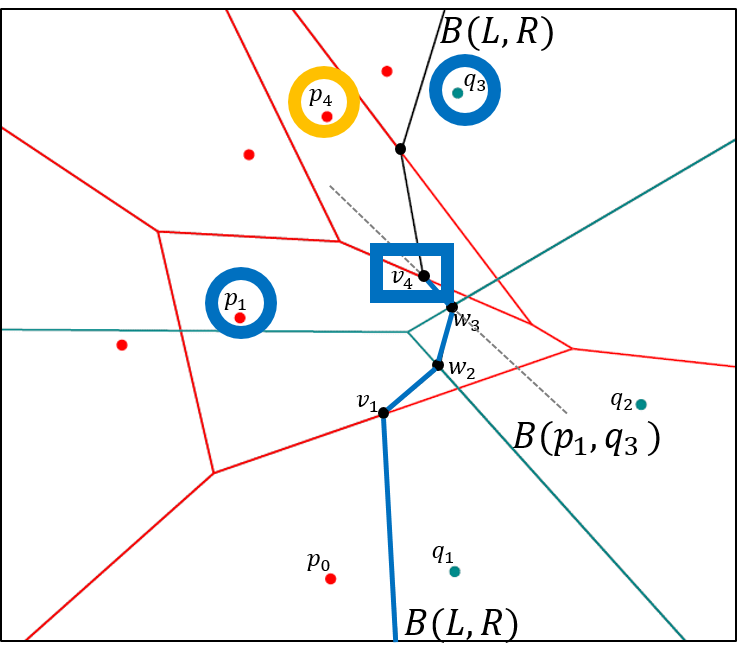

The lecture deals with topics from algorithmic geometry. These include, for example: Voronoi diagrams, algorithmic motion planning for robots, visibility in polygons, convex hull, lower contour of line segments and functions, sweep line method and applications, geometric data structures: dynamisation, k-d-tree, range tree, priority search tree.
Prior knowledge
Sufficient understanding of data structures and algorithms (Bachelor lecture).
Bachelor module information
Algorithms and Complexity, V3 + Ü2 SWS, 6 ECTS credits
Lecturer
Type of course
The course will take place in presence.
Dates
Examination
- The examinations are oral examinations.
- The content includes all exercises and all lectures.
Coursework
- Every week you will receive a homework sheet in PANDA.
- The homework is completed in groups of 2-5 people.
- The homework sheet will be graded. There are no points for plagiarism. You must achieve 30% of the points in order to take the exam. In this way you will receive the course credit.
Literature
Algorithmic Geometry
Rolf Klein, Springer-Verlag, 2005.
Computational Geometry: Algorithms and Applications
Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars, Springer-Verlag, 2008
Computational Geometry
An Introduction, Franco P. Preparata; Springer, 1993
Lectures on Discrete Geomtetry
Jiri Matousek, Springer-Verlag, 2002.
Handbook of Discrete and Computational Geometry
Jacob E. Goodman, Joseph O'Rourke, CRC Press, 1997.
