Algorithmische Geometrie

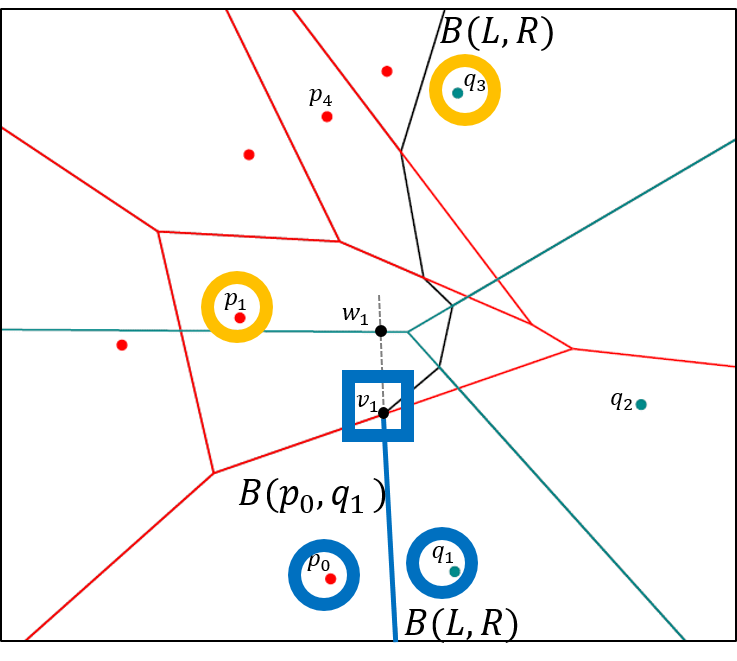
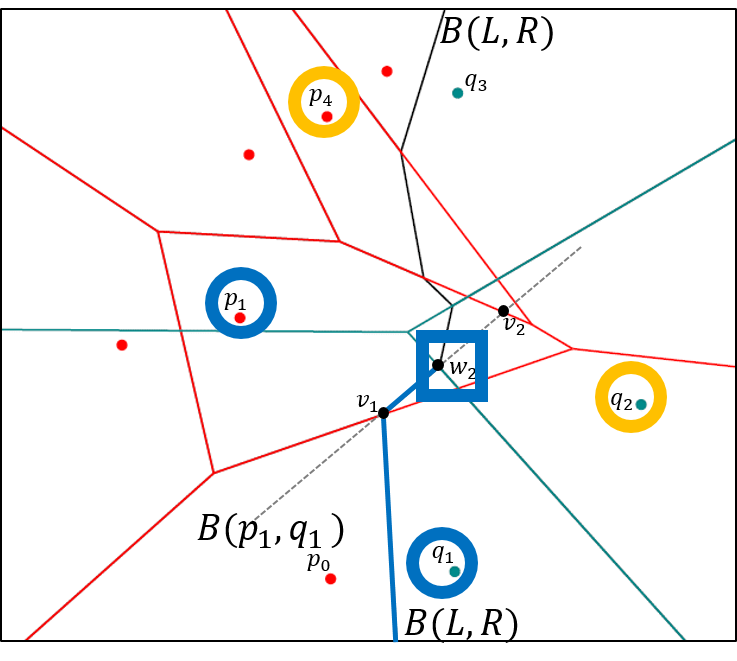
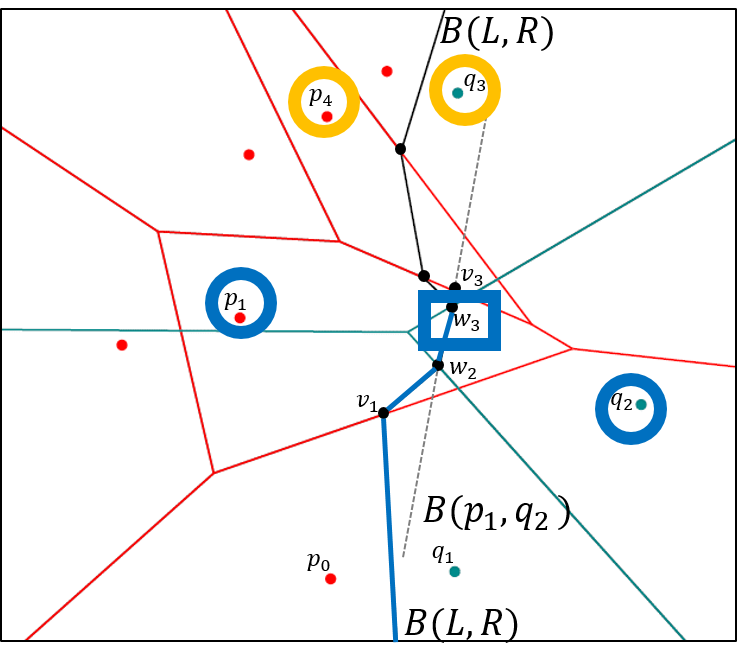
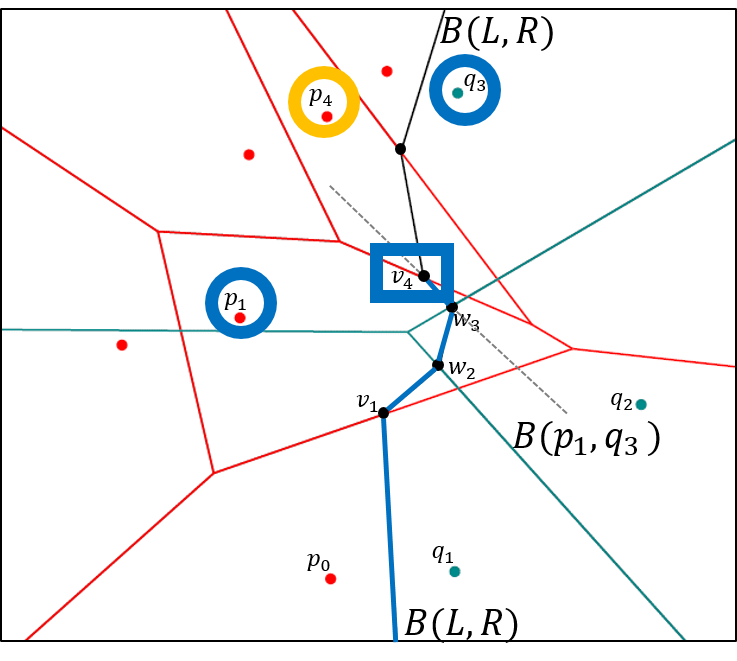
Die Vorlesung behandelt Themen aus der algorithmischen Geometrie. Dazu gehören zum Beispiel: Voronoi-Diagramme, algorithmische Bewegungsplanung für Roboter, Sichtbarkeit in Polygonen, konvexe Hülle, untere Kontur von Liniensegmenten und Funktionen, Sweepline-Methode und Anwendungen, geometrische Datenstrukturen: Dynamisierung, k-d-tree, Bereichsbaum, Prioritätssuchbaum.
Vorkenntnisse
Ausreichendes Verständnis von Datenstrukturen und Algorithmen (Bachelor Vorlesung).
Bachelor Modulinformationen
Algorithmen und Komplexität, V3 + Ü2 SWS, 6 ECTS Credits
Dozent
Veranstaltungsform
Die Veranstaltung wird in Präsenz stattfinden.
Termine
Prüfung
- Die Prüfungen sind mündliche Prüfungen.
- Der Inhalt umfasst alle Übungen und alle Vorlesungen.
Studienleistung
- Jede Woche erhalten Sie in PANDA einen Hausaufgabenbogen.
- Die Hausaufgaben werden in Gruppen von 2-5 Personen gelöst.
- Der Hausaufgabenbogen wird bepunktet. Für Plagiate gibt es keine Punkte. Sie müssen 30% der Punkte erreichen, um an der Prüfung teilnehmen zu können. Auf diese Weise erhalten Sie die Studienleistung.
Literatur
Algorithmische Geometrie
Rolf Klein, Springer-Verlag, 2005.
Computational Geometry: Algorithms and Applications
Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark Overmars, Springer-Verlag, 2008
Computational Geometry
An Introduction, Franco P. Preparata; Springer, 1993
Lectures on Discrete Geomtetry
Jiri Matousek, Springer-Verlag, 2002.
Handbook of Discrete and Computational Geometry
Jacob E. Goodman, Joseph O'Rourke, CRC Press, 1997.
