Pair­ing-based Cryp­to­graphy

Pairings are bilinear maps that enable the realization of several cryptographic primitives. Pairing-based cryptography offers approaches for numerous interesting problems, such as

• Attribute-based cryptography
• Anonymous group signatures and reputation systems
• Fine-granular access control systems (Anonymous Credential Systems) 

Pairing-based cryptography was first known and utilized in the field of identity-based cryptography. Identity-based cryptography deals with special asymmetric encryption and signature schemes. In identity-based schemes, the public key can be directly derived from the owner's identity. For example, this would allow you to encrypt an email using a key locally derived from the recipient's email address. Hence there is no need for the usual process of contacting a central key authority to retrieve the recipient's public key. Instead, the key authority is used to generate the private keys, with the added benefit that it only has be contacted once by every user. Since the key authority generates all private keys in such a system, it represents an especially lucrative target for malicious attacks.

In our group, we develop new schemes in the field of pairing-based cryptography. Furthermore, we analyze implementations of such schemes with respect to efficiency and security.

Development of so-called functional encryption schemes is one of the main visions of modern cryptography. These encryption schemes should overcome the main disadvantages of conventional encryption schemes, namely that data is encrypted for a certain addressee and the access to the encrypted data is all or nothing. In the context of functional encryption schemes, every user receives a secret key which is parameterized with a certain function according to the access rights of the user. The data is encrypted only once and the user learn only the evaluation of their function on data and not necessarily the data themselves. While in general it is difficult to even just define the security requirements for this kind of encryption schemes, efficient encryption schemes for different restricted classes of functions are known. Attribute-based encryption (ABE) is a special case of functional encryption.

An attribute-based system requires a central authority which sets the system up and provides the user with their secret keys. In key-policy ABE (KP-ABE), the owner of data defines a subset of predefined attributes for data and encrypts it once using this set. In order to access the encrypted data, every user in the system receives a user secret key provided with an access policy according to the rights of the user. The key policies are Boolean formulas over predefined attributes. A user will be able to decrypt a ciphertext if and only if the attributes of the ciphertext satisfy the policy of his/her key. For ciphertext-policy ABE (CP-ABE) the roles of attributes and policies are reversed. That is, the data is encrypted under an access policy and the keys are provided for sets of attributes. Systems based on ABE have to model the access rights of the user in terms of attributes and access policies depending on concrete scenarios and concrete access pattern.

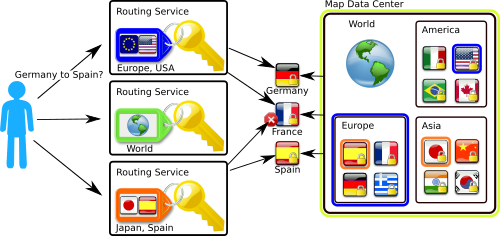
In our example, the manager of Map Data Center wants to ensure fine-grained access control to the road maps for its customers (routing services). Therefore, restricting access to the full data base, to the maps of continents, and to the maps of each single country will be realized. Each map is encrypted once with an appropriate policy. For example, the map of Germany's roads is encrypted with the policy "World OR Europe OR Germany". Every customer who gets a key with one of the attributes "World", "Europe", or "Germany", will be able to decrypt the appropriate ciphertext and obtain access to Germany's road maps. Thus, the access control is managed by the encryption itself.

In standard signature schemes, the sender computes a signature on his message using his secret key. The receiver can check, using the signature and the sender's public key, that the message was indeed composed by the sender and that it was not modified in transit. To achieve this, the public key must uniquely identify the sender. However, in many scenarios this strict identification is not necessary or even desirable. Whenever an application only needs assurance that the sender belongs to a certain group of possible senders, anonymous group signatures can be used.

Anonymous group signatures allow each member of a group to sign messages without disclosing their identity. For this, each group member gets their own private key that is associated to the group's public key. In contrast to standard digital signature schemes, the message receiver can only check whether some group member signed the message, but not which specific member did it. The actual signer can only be determined by a special entity in the system (the group manager).

Besides anonymity, other properties of group signatures play an important role in some applications. For example, it may be useful to restrict the number of messages that each group member can sign. Furthermore, techniques for revoking group membership are important. In particular, these and other extensions of group signatures can be used to construct anonymous reputation systems.

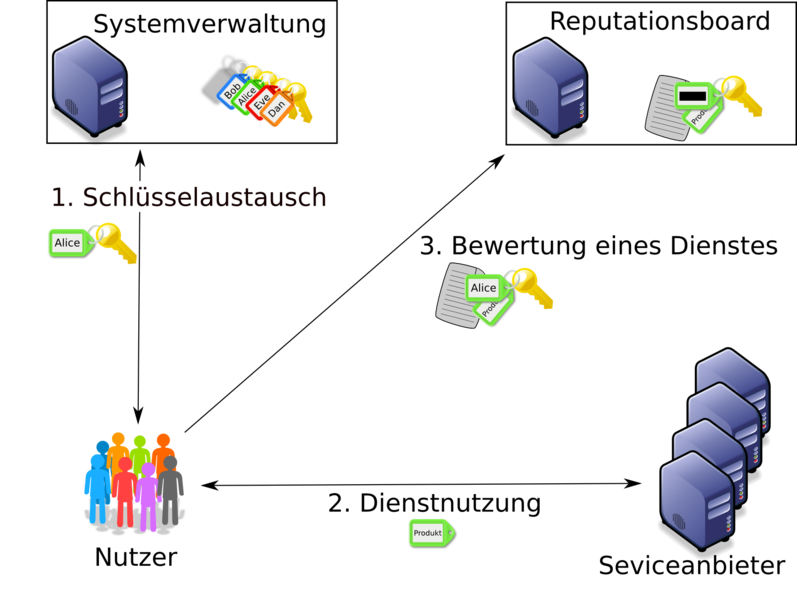
Reputation systems are an important tool to allow customers and providers of goods and services to gather useful information about past transactions. In order to receive trustworthy, reliable, and honest ratings, a reputation system should guarantee the customer anonymity and at the same ensure that no customer can submit more than one rating. Of course the ratings should be publicly verifiable by third parties.

Some of the required properties for reputation systems are already known for group signatures. Some, however, are not. For example, a reputation system does not consist of a single group, but rather there is a group for each rateable product (or service). For the security of reputation systems these different groups cannot be analyzed in isolation.

The goal of this research area is the extension of group signature schemes and the construction of anonymous reputation system on the basis of group signatures.

How can you assure a pharmacist that you have a prescription without revealing your identity? How can you show your driver's license without revealing your name? Such scenarios can be realized with anonymous credential systems. In such systems, users obtain credentials that certify attributes. With a credential, a user can access certain resources or services without revealing his identity. For this, he needs to prove that he is in possession of a credential with attributes that fulfill the resource's or service's access policy. We are interested in anonymous credential systems that support complex access policies.

In order for an anonymous credential system to be considered secure, the user must be able to access a resource without revealing his identity. Besides anonymity of users, credential systems must also make sure that users cannot collude and combine their attributes. A group of users must not be able to access to a resource for which none of the users (individually) have access to. Constructions of anonymous credentials usually rely on - among others - pairings and digital signatures.

The goal of this research area is to construct provably secure anonymous credential systems that support complex access policies.

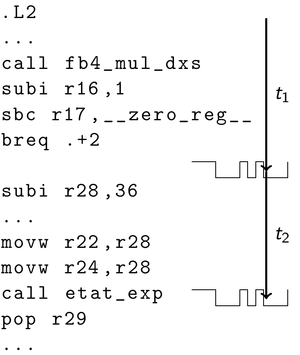
Because of the many applications of elliptic curves and pairings, increasingly more efficient algorithms to compute pairings have been developed in recent years. By now, pairings can even be computed in reasonably quickly on resource-restricted systems such as chip cards. This is particularly interesting if we want to defend against attackers with physical access to hardware executing computations that depend on a secret key. There are several ways to physically attack hardware which are usually not in the scope of formal security proofs. A physical attacker may try to gain information about the secret key by exploiting side channels. For example, the attacker may actively manipulate an algorithm's execution, or passively measure power consumption and running time. 

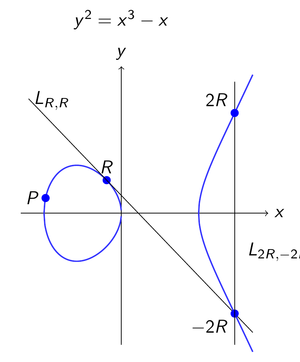
Pairings are defined on subgroups of elliptic curves over finite fields. These structures are also the basis for elliptic curve cryptography. There are already many theoretical and practical results on side-channel reistant elliptic curve cryptography. In part, these can be applied to pairing-based cryptography. For example, fault injection attacks on elliptic curve cryptography can be applied to pairing-based cryptography. For passive attacks, analysis methods for extracting information from power consumption can be applied as well. However, what cannot be easily applied to pairing-based cryptography are answers to the question "what manipulations are useful for an attacker?" and "how do I derive a secret key from data gathered through side channels?". This is because of the higher algorithm complexity and the role of the secret key for computations.

The goal of this research area is to improve security of pairing-based cryptography implemenations, to identify relevant side channels and to design efficient countermeasures against physical attackers.